首页 > 科技快讯 > Netflix是如何做决策的？（四）：漏报与功效

Netflix是如何做决策的？（四）：漏报与功效

晰数塔互联网快讯
2021-12-11 08:46

神译局是36氪旗下编译团队，关注科技、商业、职场、生活等领域，重点介绍国外的新技术、新观点、新风向。

编者按：决策是行动的指南。不管是个人还是企业，每天都要面临着无数的决策。决策的好坏会对结果产生巨大影响，如何做好决策是每个人都要上的一门必修课。在Netflix这里，他们采用了一种以实验为导向的决策流程，先小范围地对不同方案进行测试，根据对比效果调整，从而摸索出普遍适用的决策。他们为此还在官方技术博客推出了关于Netflix如何用A/N测试做出决策的系列文章。本文来自编译，是系列文章的第四篇。后续文章还将介绍实验在 Netflix 中的作用、Netflix对基础设施的投资是如何为实验提供支撑和扩展的，以及 Netflix内部实验文化的重要性。

划重点：

功效给出的是特定实验设计和规模下真阳性的概率

提高功效的手段一般有三种：增加效应量、扩大样本规模、减少基础总体指标的可变性

约定俗成的功效一般是80%

误报与漏报不能同时减少

Netflix 是如何做决策的？（一）：介绍

Netflix是如何做决策的？（二）：什么是 A/B 测试？

Netflix是如何做决策的？（三）：误报与统计显著性

在《第 3 篇：误报与统计显著性》，我们定义了在解释测试结果时可能会出现的两种错误类型：误报与漏报。然后，我们用抛硬币这个简单的思维练习来建立对误报和相关概念（如统计显著性、p 值与置信区间）的直觉。在这篇文章里，我们将对漏报与统计功效的相关概念做同样的事情。

图 1：跟第 3 篇一样，我们还是拿抛硬币这个思维练习，比如这个凯撒·奥古斯都面朝上的游戏，一边建立起对核心统计概念的直觉。

漏报与功效

当数据没能表明治疗组与控制组之间存在有意义的差异，但实际上差异是存在的时候，就会出现漏报（假阳性，false positive）。继续第 3 篇里面的示例，漏报对应于把猫的照片标记成“没有猫”。漏报与功效这个统计概念密切相关，功效给出的是特定实验设计和规模下真阳性的概率。事实上，功效不过是1减去漏报率而已。

功效牵涉到的是对有关世界实际状态的特定假设的可能结果——跟我们在第 3 篇里面首先要假设零假设为真来定义显著性类似。为了建立对功效的直觉，我们不妨回到第 3 篇里面举过的那个抛硬币的例子，目标是用计算抛 100 次硬币时出现正面的比例这个实验来确定硬币是不是均匀的。在硬币是均匀的零假设下，结果分布如图 2 所示，用黑色标记。为了让那张图解释起来更容易些，我们对直方图的顶部进行了平滑处理。

如果硬币不均匀的话，这个实验会出现什么情况？为了让这个思维练习更具体些，我们不妨看看当我们有一枚硬币出现正面的平均概率为64% 时会发生什么（为什么要选这个数字后面我们会解释的）。因为我们的实验存在不确定性或噪音，所以我们不指望抛 100 次能够正好看到有 64 次为正面。但就像假设硬币是均匀的零假设一样，如果这个特定的替代性假设为真，我们就可以计算粗所有可能的结果。这种分布如图 2 的红色曲线所示。

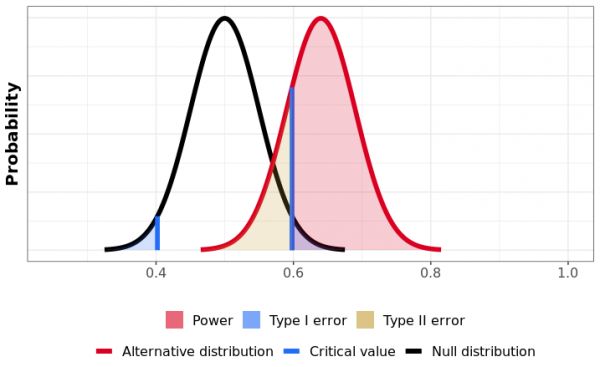
图 2：用掷100 次硬币然后计算正面朝上的占比这个例子来说明功效。黑色和红色虚线分别显示的是假设出现正面概率为 50%（零假设）与 64%（替换假设的特定值）的结果分布。在本例中，该替代方案的功效为 80%（红色阴影）。

从上图看，功效是替代分布（红色）里面超出零假设（蓝线和黑色曲线；参见第 3 篇）临界值的部分。在本例中，替代分布（红色）有80%落在了较高的蓝色线（该线划定的是右侧拒绝区域的临界值）的右侧。假设这枚硬币正面朝上事实上的概率是 64%，那么本次测试的功效就是 80%。为了完整起见，替代分布（红色）还有一小部分落在左侧拒绝区域内（蓝色短线的左侧）。

检验的功效跟特定的假设的效应量相对应。在我们的例子里面，如果这个不均匀的硬币正面朝上的实际概率为 64%，则检测硬币是否不均匀的功效为 80%。解释如下：如果硬币正面朝上的概率为 64%，并且我们反复进行抛 100 次的实验并按照 5% 的显著性水平做出决定，那么我们每5次实验得出拒绝硬币是均匀的零假设的结论中大约有 4 个是对的。这些重复的实验当中有 20% 会导致漏报：也就是我们不会拒绝硬币是均匀的零假设，哪怕其实硬币是不均匀的。

提高功效的办法

在设计 A/B 测试的时候，我们首先要确定显著性水平（约定为 5%：如果治疗与控制之间没有差异的话，我们有 5% 的可能性出现误报），然后我们设计实验来控制漏报。我们可以通过三个主要手段来提高功效，减少漏报的可能性：

效应量。简而言之，效应量（A 组和 B 组之间的指标值差异）越大，我们能够正确检测到这种差异的概率就越高。为了建立直觉，不妨假设做个实验来确定硬币是否不均匀，我们要收集的数据是抛 100 里面出现正面的比例。现在设想两种场景。在第一种情况下，正面朝上的真实概率为 55%，而在第二种情况下为 75%。直观上（以及数学上！）我们的实验更有可能在在第二种情况下将硬币识别为不均匀。正面的真实概率与 50% 的零假设相差更大，所以实验产生的结果更有可能落在拒绝区域内。在产品开发的环境下，我们可以通过我们大胆增加要测试的假设的增量来增加指标变动的预期幅度。增加效应量的另一个策略是在会员满意度可能有更大的提升空间的产品新领域进行测试。也就是说，通过实验学习的乐趣之一是其中会有惊喜元素：有时候，看似微小的变化可能也会对最高级别的指标产生重大影响。

样本规模。实验的单位越多，功效越高，越容易正确识别较小的效应。为了建立直觉，再设想去做个实验来确定硬币是不是不均匀，我们要收集的数据是抛固定次数下正面朝上的比例，而正面朝上的真实概率为 64%。然后考虑两种情况：第一种情况，我们抛20 次硬币，第二种情况，我们抛100 次硬币。直观上（以及数学上！）而言，我们的实验更有可能在第二种情况下把硬币识别成不均匀。因为在有了更多数据的情况下，实验的结果会更接近 64% 的真实概率，而基于硬币是均匀的假设下，结果应该集中在 0.50 左右，导致拒绝区域侵占掉 50% 的值。在这些效应相结合下，因此如果拿不均匀的硬币做实验，数据越多，结果就越有可能落入该拒绝区域，从而产生真阳性。在产品开发环境里，我们可以通过给测试分配更多的会员（或其他单位）或减少测试组的数量来提高功效，不过在每次测试的样本量与同时可以进行的不重叠的测试数量之间需要做出权衡（样本量大，可进行的测试数就少）。

基础总体指标的可变性。指标在待测试总体里面越同质化，就越容易正确识别真实效果。这个的直觉有点难以理解，我们那个简单的抛硬币例子终于没法解释了。假设在Netflix这里，我们要进行一项测试，目的是看看某些减少延迟（比方说成员按下播放与开始视频播放之间的延迟）的措施是否有效。鉴于大家用来访问 Netflix 的设备与互联网连接的多样性，在我们的用户当中这个指标会存在很多自然的可变性。因此，如果测试治疗组的结果只是延迟指标小幅减少的话，是很难识别成功的——因为不同会员之间可变性的“噪音”比信号要强。相比之下，如果我们对采用类似网络连接与类似设备的一组会员进行测试的话，那么强度不大的信号就会更容易识别——因为可能会压制信号的噪音更少了。在 Netflix 这里，我们花费了大量时间来构建利用这种直觉的统计分析模型，并通过有效降低可变性来提高功效；相关做法的技术说明，请参见此处。

为合理和有意义的效应设定功效

功效和漏报率是假定效应量的函数。就像 5% 的误报率是一个被广泛接受的约定一样，功效的经验法则是将 80% 的功效定为合理且有意义的效应量的目标。也就是说，我们假设了一个效应量，然后设计实验（主要是设置样本大小），这样的话，如果治疗体验的真实影响如我们假设一样的话，在80%的时间内测试都能够正确地识别出效应的存在。在 20% 的时间内测试结果会是漏报：也就是说其实是有效果的，但我们对测试观察到的结果不在拒绝区域内，所以我们无法得出有效应的结论。这就是为什么上面的例子用了 64% 正面朝上的概率：抛100 次的实验功效为 80%。

合理的效应量由哪些东西构成这个问题很棘手，因为测试可能会产生意外结果。但是结合领域知识与常识一般可以提供可靠的估计。在测试历史悠久的领域，比方说帮助Netflix 会员选择适合自己的内容的优化推荐系统，我们对测试大致产生的效应量（不管是阳性还是阴性）已经有了明确想法。在对过去的效应量以及分析策略有了了解之后，我们就可以设置样本大小，来确保测试对合理的指标变动具有 80% 的功效。

不管是在这个实验设计阶段还是在决定往什么地方做出努力时，第二个考虑因素是要确定什么对用来决定测试的主要指标产生了有意义的效应。怎么才算有意义要取决于实验的影响领域（会员满意度、播放延迟、后端系统的技术性能等），以及与新产品体验相关的潜在工作或成本。我们不妨假设如果效应量小于主要指标 0.1% 的变化的话，则支撑新产品功能的成本就大于收益。在这种情况下，通过测试来检测指标是不是发生了 0.01% 变化就几乎没有意义，因为成功识别这种效应量并不会导致决策发生有意义的变化。同样地，如果对特定创新领域所做测试观察到的效应量对用户体验或业务来说始终都无关紧要的话，则表明我们可以把实验资源部署到其他更有效的地方了。

总结

本系列的第 3 篇和第 4 篇重点是对用来分析测试结果的核心概念进行定义并建立相关直觉：其中包括了假阳性（误报）、假阴性（漏报）、统计显著性、p 值，以及功效。

关于实验，有个事实也许会令人不安，那就是我们不能同时最大限度地减少误报和漏报。事实上，误报和漏报会相互制约。如果我们采用更严格的误报率，比方说 0.01%的话， A 和 B 之间没有差异的测试的误报数量就会减少——但这样也会降低测试的功效，增加那些存在有意义差异的测试的假阴性（漏报）率。用 5% 的误报率以及 80% 的功效是约定俗成的惯例，可以在限制发现错误与取得真正发现之间取得平衡。然而，在假阳性（或假阴性）会带来更大风险的情况下，研究人员可能就会抛开这些经验法则，好尽量减少某种类型的不确定性。

我们的目标不是要消除不确定性，而是去理解和量化这种不确定性，以便做出合理的决策。在很多情况下，A/B 测试的结果需要细致入微的解释，实际上测试结果本身也只是商业决策的一个输入。在下一篇文章里，我们会介绍怎么用测试结果建立起对决策的信心。

译者：boxi。