首页 > 科技快讯 > 19世纪末的数学高峰：庞加莱的自守函数研究

19世纪末的数学高峰：庞加莱的自守函数研究

晰数塔互联网快讯
2025-04-10 08:10

本文来自微信公众号：返朴（ID：fanpu2019），作者：金威

在高斯（Carl Friedrich Gauss，1777-1855）、黎曼（Bernhard Riemann，1826-1866）等数学大家涌现的19世纪将要结束之时，数学领域迎来了它的又一次统一和革新，这就是庞加莱（Henri Poincaré，1854-1912）和克莱因（Felix Klein，1849-1925）等数学家对自守函数（automorphic function）的研究。所谓自守函数，就是一个复函数，它在复平面分式线性变换群(2，ℂ)的一个离散子群变换下保持不变：即对定义域上的每个复数，有()=(∘)，其中每个群元∈可以写成的形式。

由定义可见，自守函数是一种高度对称的复变函数。而要想更深入地理解其深刻意义，当然不能仅仅从定义出发，而需要比较全面地了解它的“过去、现在和未来”。

在历史上，自守函数理论的来源是多方面的：有分析学中的（1）椭圆积分和椭圆函数[主要研究者（下同）：欧拉（Leonhard Euler，1707-1783）、高斯、阿贝尔（Niels Abel，1802-1829）、雅可比（Carl Jacobi，1804-1851）]；（2）常微分方程理论和单值化群[欧拉、高斯、富克斯（Lazarus Fuchs，1833-1902）]；和（3）复变函数论[柯西（Augustin-Louis Cauchy，1789-1857）、黎曼、魏尔斯特拉斯（Karl Weierstrass，1815-1897）、施瓦兹（Hermann Schwarz，1843-1921）]，兼及代数学中的（4）群论[阿贝尔、拉格朗日（Joseph-Louis Lagrange，1736-1813）、伽罗瓦（Évariste Galois，1811-1832）、克莱因）]和几何学中的（5）非欧几何[高斯、鲍耶（János Bolya，1802-1860）、罗巴切夫斯基（НиколайИвановичЛобачевский，1793-1856）]及其模型[贝尔特拉米（Eugenio Beltrami，1835-1900）、克莱因、庞加莱、刘维尔（Joseph Liouville，1809-1882）]。

而庞加莱和克莱因的工作不仅集前人之大成，而且一举将数学中的分析、代数和几何等几大领域统一起来，开辟了自守函数这个位于交叉点上的新领域，并为之后的单值化定理做好了直接准备。

因为篇幅所限，本文将侧重于介绍庞加莱在自守函数相关领域的贡献，但必须指出，克莱因在本领域的工作也是丰富多彩和独树一帜的（可参考[1]）。另外因为笔者个人水平和精力所限，加之时移世易，本文必然挂一漏万，请各位读者不吝指正。

1、序曲：自守函数前史

首先，我们回顾一下在庞加莱的工作之前，数学中相关各领域的历史状况，以便了解自守函数为何能将这些领域统一起来。在此处，笔者尽力将当时的相关背景做一些概括和提要，并将它们按照领域尽量分割开来。但读者将看到，在数学这个整体而不是数学的各个“部分”之中，存在着几条相互紧密交织的线索，它们只能大致在思维中再现，但我们绝不可能按照人物、时代或者领域将这几条线索截然地分开。

1.1自守函数的来源：分析方面

自守函数的第一个来源是分析学。19世纪，分析学继续发展出多个领域，包括单复变函数、微分方程、微分几何和变分法等，这些分析学科成为整个数学的核心部分。而自守函数理论与其中的单复变函数理论（包括其中的椭圆积分和椭圆函数理论）和微分方程理论的关系最为密切。其中，椭圆函数是自守函数的重要例子，而自守函数则是其非平凡推广，其背后的舞台则是复变函数理论，尤其是经黎曼的几何观点发展后的复变函数论；常微分方程的单值群是自守函数不变性条件的自然来源之一；而非欧几何及其等距变换群则刻画了自守函数不变性条件的几何本质。

（1）椭圆函数及一些相关函数：

古典微积分理论中提出了以下问题：

（1）研究初等函数（包括有理函数）的不定积分，将其尽量表示为初等函数；

（2）如果无法表示为初等函数，就尝试研究各种初等函数积分（不定积分和定积分）的相互关系和各自性质。

椭圆函数理论肇始于对椭圆积分的研究。所谓椭圆积分，就是数学家为求椭圆弧长等问题出发而引入的形如的积分，其中是有理函数，而()是无重根的三次或四次多项式函数。它首先由欧拉和勒让德（Adrien-Marie Legendre，1752-1833）引入，当时他们主要是在实数域中研究椭圆积分。后来，高斯（在1820年左右，但未发表）、阿贝尔和雅可比（从1823-1826年左右开始）对椭圆积分（如）在复数域中的行为开展了研究，发现了一些关系，尤其是考虑了其反函数——椭圆函数。他们发现椭圆函数在复数域上有双周期性，这是一个里程碑式的发现。一个较为初等的类比是：反正弦函数的反函数——大家熟知的正弦函数=sin是单周期的。

椭圆函数理论引发的进一步问题有：

（1）研究椭圆函数是否有更优美的性质？

（2）从更高的观点解释椭圆函数的双周期性；

（3）进一步研究双周期函数的一般性质；

（4）一般地给出双周期函数的构造。

在1860年左右，在学习阿贝尔和雅可比著作的基础上，魏尔斯特拉斯研究了椭圆函数的幂级数展开，构造了著名的椭圆函数，并证明每个椭圆函数都可以表示成及其导数的有理函数。此外，凯莱（Arthur Cayley，1821-1895）、布尔（George Boole，1815-1864）等从1840年开始，又用不变量观点证明了阿贝尔研究椭圆函数时得到的一些结论。此时，椭圆函数双周期性之下蕴藏的更深刻意义还远未被阐明，这个任务将由黎曼完成。

椭圆函数在19世纪又被戴德金（Richard Dedekind，1831-1916）等用于数论方面的研究。埃尔米特（Charles Hermite，1822-1901）、克罗内克（Leopold Kronecker，1823-1891）、布里奥斯奇（Francesco Brioschi，1824-1897）等人则在此基础上，使用椭圆函数求解五次代数方程。克莱因在此问题上的贡献尤为值得注意，他将椭圆函数、正二十面体、群论和微分方程熔于一炉，其研究堪称珍品，见[6]。

所定义的基本区域更复杂的一类函数，是所谓的“三角形函数”[Triangle function，请勿与“三角函数”（trigonometric function）混淆]：黎曼和施瓦兹在研究（与超几何方程相关的）常微分方程时，发现其每个特解()是从所在的上半复平面到平面的一个共形映射，其象集为一个以圆弧为边的曲线三角形。使用复变函数中的反射原理，可以将其定义域扩张到整张复平面，其构造过程是黎曼映射定理的一个重要例子。而其反函数()的定义域可以用关于三角形边的反射（及其复合）扩张到半平面或圆。

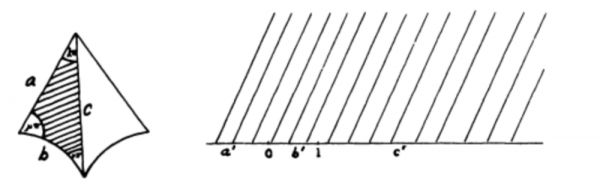
图2三角形函数示意图，左侧对应变量，右侧对应变量。图源：参考文献[14]

此外，当这里的离散子群为(2，ℤ)时，对应的函数称为模函数。由于其在数论方面的背景和动机——例如研究虚二次域的阿贝尔扩张和整正定二次型的分类问题等，模函数和椭圆函数也先后被高斯、爱森斯坦（Gotthold Eisenstein，1823-1852）、霍尔维茨（Adolf Hurwitz，1859-1919）、埃尔米特、戴德金等数学家所研究。

图3模函数所对应的复平面划分，每个色块为一个“基本区域”。此图也称为戴德金镶嵌（Dedekind tessellation），由戴德金在1877年发现。

例如，仅仅是高斯一人，就曾经从三种不同的动机研究过椭圆函数：（1）算术-几何均值；（2）整正定二次型理论；（3）对双扭线的研究。

从三角函数、双曲三角函数等简单的单周期函数，到双周期的椭圆函数，再到三角形函数、模函数等对称性更为复杂的函数，都是自守函数的经典例子。由此可见，即使仅仅在函数论意义上，自守函数的来源就已十分自然和丰富；另一方面，自守函数作为这些重要函数的自然而非平凡的推广，必然是富有生命力的。

（2）复变函数论：

在微积分发展以后，复变函数理论首先起源于如下朴素的问题：

（1）如果在复数域上做微积分，会得到什么有趣的结论？换句话说，（单）复变量函数有什么引人注目的性质？

（2）应该如何（用怎样的观点和理论工具）研究复变量函数？

（3）建立起复变量函数的一般理论后，它能为我们提供什么新的视角和观点？它们又有哪些具体应用？

单复变函数理论有三大理论路线，它们都从不同的角度回应了以上问题。这三条路线正是柯西的积分和函数论方法、魏尔斯特拉斯的幂级数方法和黎曼的几何方法。其中，黎曼在复变函数领域的贡献最值得注意，他以内蕴和几何化的观点革新了复变函数理论：定义了多值解析函数的黎曼曲面并将其应用到椭圆函数和椭圆积分理论中。（之后庞加莱以自己超人的数学能力和独创性，逐渐借鉴并先后掌握了这三种方法，并将其应用到自守函数和单值化定理的研究中。）

我们回到黎曼对椭圆函数理论的研究思路。首先，黎曼通过内蕴方式（类似于黎曼几何中的哲学）将复解析函数对应到一个曲面，这个曲面由复平面的若干拷贝沿函数分支点的一些连线切开后粘合而成（即复平面的分支复叠），称为这个函数的黎曼面。此时原本的“多值”函数就成为黎曼面上的单值函数。

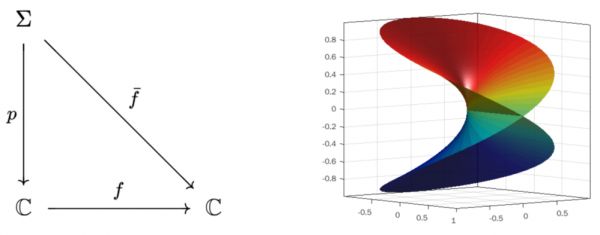
图4左图：如果:ℂ→ℂ是一个“多值函数”（例如“开平方根”：除零点以外，每个复数均会有两个不等的根），则其黎曼面构造给出了一个曲面Σ及分支复叠映射:Σ→ℂ，使得其复合为单值解析函数（即成为真正的映射）。实际上Σ解析同胚于函数的图（graph）。右图：函数的黎曼面（局部示意图），它解析同胚于复曲线{(，)|=2}。

然后，考虑椭圆积分中的被积函数2=()（其中()是无重根的三次或者四次多项式函数）的黎曼面——它是一个环面。而椭圆积分可以看成定义在环面上的积分，根据不同的积分路径（的同伦类）选取，可以得到许多不同的积分值，它们彼此相差两个复数的整数倍线性组合：11+22，此处1和2分别对应变量绕环面的经线和纬线转一周得到的积分值；最后，如果考虑椭圆积分的反函数=Φ-1()，那么它就是双周期的：。在此观点下，椭圆积分反函数的双周期性变得十分显然。因此，从几何观点看，椭圆函数对应的黎曼面是一个环面，是一条“亏格为1的复1维曲线”，因此它也被称为“椭圆曲线”。

黎曼还指出：一个亚纯函数的形态在本质上由其奇点决定。黎曼还研究了多连通区域的“连通数”及其与亏格的关系等，这是拓扑学的早期起源之一。

另外黎曼在博士论文中还提出了“黎曼映射定理”，即复平面上两个单连通开区域必然全纯等价，它是单值化定理的一个特例。不过文中黎曼的证明用到了当时尚未严格证明的狄里克莱原理，因此是不够严格的。

（3）常微分方程

从18世纪开始到19世纪，数学家和物理学家开始普遍使用常微分方程和偏微分方程研究数学物理现象。而对于纯数学，有以下问题：

（1）尽量给出常微分方程的解析解；这些解有怎样的性质？

（2）常微分方程常常无法写出解析解。在此情况下，应当怎样研究常微分方程？

所谓的超几何方程，是关于复变函数()的二阶微分方程。它始于欧拉和高斯的研究，其解为著名的超几何函数。后来，黎曼和施瓦兹在研究此方程的过程中，发现了上文中提到的三角形函数，研究的大致思路如下：

对于关于复变函数()的二阶微分方程”+1′+2=0，因为它是二阶的，故可设其两个线性无关的基本解为1和2。首先，如果令变量绕着奇点附近的闭路径环绕一圈，函数就需要经过解析延拓而变到另一单值分支，从而变为和。如果设两基本解的比值为，则该比值在沿闭路径环绕后（经过解析延拓）即变为。让变量在复平面上绕着奇点走遍所有可能的闭路，对应的所有变换即构成一个群，称为此方程的单值化群（monodromy group）。这里就出现了分式线性变换！而单值化群必然是分式线性变换群的子群。方程的解()的反函数()是关于单值化群的自守函数。

同时，布里奥（Charles Briot，1817-1882）和布凯（Jean-Claude Bouquet，1819-1885）则用奇点理论的观点研究常微分方程。

在此之后，富克斯一般地研究了复数域上的（高次）常微分方程，并证明了一些定理，包括微分方程的解只会在系数函数的奇点处出现奇异性。但富克斯的研究是不完整的，其主要遗留问题在于：解在初始定义域上多次沿边界反射延拓后，各区域在整体上是否有重合的部分（其局部情形已被富克斯解决）。

此外，庞加莱还发展了常微分方程的定性理论（与他在自守函数与微分方程方面的工作，例如下文所述的第五篇长文有关）。

1.2自守函数的来源：代数学

在代数领域，自守函数主要和群论关系密切。在历史上，群论有三个主要来源：（1）数论中欧拉、高斯等对（同余）模算术的研究；（2）在高斯、鲁菲尼（Paolo Ruffini，1756-1822）、拉格朗日、阿贝尔和伽罗瓦研究一般系数代数方程的根式解工作之后，群的观点被建立起来，并开创了著名的伽罗瓦理论；（3）在几何领域，克莱因基于对射影几何的研究和受非欧几何等几何理论的启发，在1872年提出埃尔朗根纲领，即“每种几何学都是研究在一定群变换下不变的几何量”，把几何学和对称性（群论）的观点深刻地联系在一起。随后，克莱因研究了二十面体的对称群与五次方程根式解之间的关系。另外，凯莱在1854年给出了群的抽象定义。

1.3自守函数的来源：几何学（非欧几何）

非欧几何起源于对欧几里得《几何原本》中的“平行公理”即第五公设的质疑。第五公设的现代叙述形式为：“过直线外一点，有且只有一条直线与已知直线平行”，这种形式源于波斯的哈亚姆（Omar Khayyam，1048-1131），他是诗人、哲学家、数学家、天文学家，被誉为“波斯的李白”。千百年来数学家对这条公设（相对于其他公设的）的无矛盾性和独立性争论不休。

高斯、罗巴切夫斯基、鲍约几乎同时发现了非欧几何，这无疑是人类数学史甚至文明史中的巨大革命。它不仅打破了欧几里得几何学的时空观，甚至在数学之外的领域，如在哲学上也产生了深远影响。（关于这次革命的意义，可参考[16]。）

在黎曼几何观点出现后，数学家们为双曲几何建立了若干不同的几何模型。庞加莱之前的双曲几何模型有：（1）贝尔特拉米在1868年提出的伪球面模型；（2）半球面模型，其空间是不含边界的上半球面，度量是=。其测地线是三维空间内垂直于平面的平面截上半球面形成的圆弧，而它向水平平面垂直投影后即得到（3）克莱因圆盘模型，位于平面的开单位圆盘上，其测地线是直线；（4）在1854年发现、后来被称为“庞加莱圆盘”的模型，其空间是平面上的单位圆盘，可看作半球面模型对其位于北极的切平面做球极投影变换（再做适当的放缩）得到，其度量为。对这个模型这个模型，黎曼曾发现了它的共形性，但是没有注意它和非欧几何之间的联系；（5）刘维尔在1850年提出的上半平面模型，其空间为不包含边界（实数轴）的上半平面，度量为，现在被称为庞加莱上半平面模型。

图6此图中水平平面为克莱因和庞加莱模型所在的单位圆盘，对应的测地线依次为黄色和红色；上半球面对应半球面模型，其测地线为蓝色。图源：wiki。

虽然贝尔特拉米、黎曼和刘维尔等人更早地得到了双曲平面中的若干模型，但庞加莱却更加敏锐地发扬了它的意义——主要是发现分式线性变换群能够保持非欧度量不变，并在自守函数的构造和研究中本质性地用到了双曲几何（详见本文第二部分），这使得非欧几何进一步进入到主流数学当中。

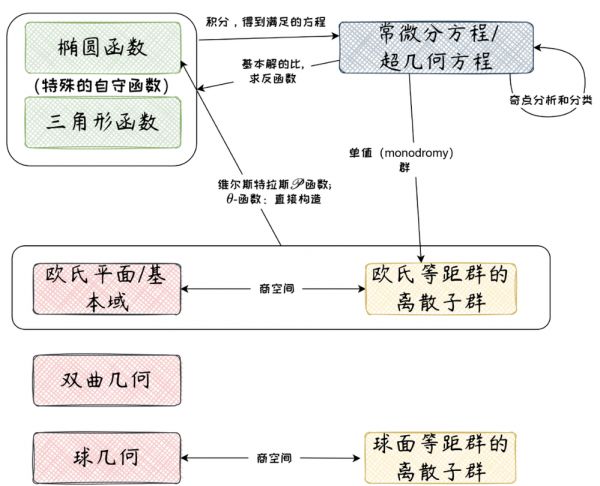
图7不同颜色表示不同领域：红色—几何；黄色—代数；蓝色—拓扑；蓝灰色—方程；绿色—分析，下同。

上述谈到的各个数学问题和领域，遍及分析（函数论和微分方程）、代数和几何等数学分支，其大致图景如图7。从图中可见，当时的分析—代数—几何相互联系的“连通分支”还集中在欧氏几何领域，非欧几何则是相对孤立的。

而庞加莱和克莱因的工作则真正地将上述各个领域有机和有力地结合起来，从而淋漓尽致地体现出数学的统一性。

2、主题（融合统一）：庞加莱及其在自守函数上的工作2.1时代背景和庞加莱的直接动机

我们首先略微回顾一下19世纪几个欧洲国家数学发展的大致背景。在工业革命后，英国在自然科学和技术方面一直较为领先，但因为其思想上的经验主义传统和社会结构产生的保守倾向，英国人更倾向于将相对较成熟的数学理论应用于科技领域。后来英国学术界觉察到了这种局限性，从而剑桥分析学派和之后的数学物理学派[格林（George Green，1793-1841）、斯托克斯（George Stokes，1819-1903）、麦克斯韦（Jame Maxwell，1831-1879）等）]应运而生；同时也产生了凯莱这样的大数学家，但在纯粹数学方面仍相对比较落后。之后，因启蒙运动和法国大革命，欧洲尤其是法国的社会面貌焕然一新，崭新的科研和高等教育体制逐渐建立起来，法国逐渐成为世界数学中心[以泊松（Siméon-Denis Poisson，1781-1840）、柯西、刘维尔等人为首）]。但从十九世纪中叶起，法国数学被后来居上的德国数学所超越，原因在于社会环境、哲学思想以及普法战争所导致的德法争霸等多重因素。19世纪的德国数学，经过狄里克莱（Lejeune Dirichlet，1805-1859）、黎曼等创建哥廷根学派，魏尔斯特拉斯、库默尔（Ernst Kummer，1810-1893）、克罗内克等创建柏林学派，以及克莱因在数学研究和数学教育上承前启后，迎来了它的辉煌时代。而当时法国数学的函数论[埃尔米特、达布（Jean-Gaston Darboux，1842-1917）、若尔当（Camille Jordan，1838-1922）等]视角则较为古典，直至十九世纪末，法国涌现出皮卡（Émile Picard，1856-1941）、阿达马（Jacques Hadamard，1865-1963）等数学家，加之庞加莱横空出世，让数学的各个分支在新的高度上获得了前所未有的统一。借此，法国数学才又重回世界数学之巅。[3，4]

庞加莱被誉为“数学家中的最后一个通才”和“20世纪最伟大的数学家之一”，其贡献涉及数学（分析、代数、几何、拓扑、代数几何、动力系统、数论）、物理学（电磁学、狭义相对论）、天体力学和科学哲学等众多领域。

庞加莱是怎样进入自守函数这个领域的呢？

其直接动机是参加巴黎科学院举办的论文竞赛。1879年，巴黎科学院征文比赛的题目是：“用某种重要方式改进单变量常微分方程理论”。庞加莱恰于此年获得博士学位，并在卡昂大学担任讲师，他当时正在思考常微分方程的问题，因而参加了征文比赛（后获得二等奖）。他的创建始于富克斯研究的局限部分，即后者的观点主要是局部而不是全局的（见本文第一部分《序曲》），因此庞加莱逐渐将观点从分析和方程扩展到几何视角，从而用更加全局的观点看待微分方程的解，并逐渐将其作为一个独立的数学对象加以研究，即在复平面的某些群作用下不变的函数。

庞加莱经过了一系列的反复尝试，取得了几次阶段性的突破。例如，在多年之后，他在其著作《科学与方法》中回忆在1880年6月的一次顿悟：

“在这时，我离开了当时居住的卡昂，参加了矿业学校（Écoles des Mines）主办的地质考察旅行。沿途的景致使我忘却了我的数学工作。到达库唐塞（Coutances）后，我登上公共马车去某个地方。当我的脚踩上踏板的一刹那，一种想法涌上我的心头，即我通常定义富克斯函数的变换等价于非欧几何学的变换，在我先前的思想中，似乎没有任何东西为它铺平道路。我没有证实这一想法；我坐在公共马车座位上，此时不可能有时间证实，而是继续进行已经开始的谈话，但是我感到它是完全确定的。返回卡昂，为了问心无愧起见，我抽空证实了这一结果。”[11，13]

在此过程中，庞加莱也与其他数学家保持着沟通，先后与富克斯、克莱因等人进行书信往来。最终，庞加莱终于将微分方程、富克斯函数及其构造方式、非欧几何（双曲平面）及其变换群真正地联系起来。

2.2庞加莱的综述：五篇长文

从1882年开始，庞加莱和克莱因均总结了各自的工作。庞加莱在《数学评论》（Acta mathematica）、《法国科学院院刊》（Comptes rendus de l’Académie des Sciences）等期刊上共发表了至少三十篇相关主题的文章[9]。下面简述一下其中在《数学学报》上发表的比较重要和有概述性质的五篇长文，其发表时期在1882-1884年，篇幅在四十多页至一百余页不等；其中前四篇的英译可参见[10]。

这五篇文章的大致内容是：第一篇长文介绍双曲几何观点，论述富克斯群和双曲圆盘/平面在该群作用下基本域的关系；第二篇借助与椭圆函数理论的类比，给出了富克斯群作用下不变的自守函数（“富克斯函数”）并研究其相关性质；第三篇将前两篇长文的研究进一步拓展到克莱因群上，即研究了克莱因群及其对应的自守函数（“克莱因函数”）；第四篇和第五篇长文则主要研究上述的自守函数与微分方程的关系，并提出进一步的问题，如自守函数的独立性等。

2.2.1《关于富克斯群的理论》

第一篇是Théorie des groupes fuchsiens，即《关于富克斯群的理论》。

对于复平面的共形变换群（莫比乌斯群）的离散子群，如果子群中的元素共同保持一个圆不变，那么这个圆就称为此群的不变圆（通过共轭，可以将这个不变圆映为实轴）。庞加莱独具只眼地发现：因为复共形变换群的实元素均保持双曲平面的长度、角度和面积，因此只要存在不变圆，就可以用平面双曲几何的观点研究该群的群作用（即此文），以及在群作用下不变的函数（主要在之后的第二篇长文中有所应用）。从而首先激发了以下问题：

从几何（度量模型）和代数（变换群）角度研究复平面/双曲平面及其商空间，并将它们关联起来。

为回答以上问题，在这篇文章中，庞加莱系统研究了双曲平面等距变换群（以下简称“双曲等距群”）的离散子群及其基本域（即在群作用下的“镶嵌单元”），以及二者的相互关系：双曲等距群的离散子群当然可以决定双曲平面在此群下的商空间，它是一个多边形，再加上多边形的边由群元素作用给出的相互粘合关系；反过来，如果给定多边形和粘合关系，并满足一定兼容性条件，就存在对应的离散子群，使得这个多边形在粘合关系下的商空间就是双曲平面在离散子群作用下的商空间，后者的对应就是所谓的“庞加莱多边形定理”。

图10：版画家埃舍尔（1898-1972）的版画《圆极限IV》（circle limit IV），又名《天堂和地狱》，及其对应的双曲平面{6，4}镶嵌，镶嵌单元为六边形。

庞加莱将双曲等距群的离散子群（或者等价地，存在一个不变圆域的复分式线性变换群的离散子群）称为富克斯群。我们知道，因为非欧几何的复杂性，双曲平面的几何及其镶嵌与对称群要比欧氏几何的版本复杂得多（例如对欧氏平面上的镶嵌，作为镶嵌单元的形状本质上只有有限几类，但双曲平面的镶嵌单元则有无限多类），所以需要介绍必要的基础。为了这个目的，庞加莱根据需要，在文中自由地使用上半平面模型和圆盘模型。但在文中他并没有引入更多的非欧几何概念，例如其中弧长和面积的计算公式。

这篇文章首先引入了上半平面变换群的正常不连续（properly discontinuous）子群，并对其进行了组合刻画（使用了群表现，即生成元/关系的观点），然后转入研究基本域和基本多边形的概念和分类，并研究了它在富克斯群作用下的行为和性质，如被群作用将边粘贴后的亏格。之后，庞加莱证明，对于满足一定条件的多边形和粘合映射，总存在对应的富克斯群，使其基本域和粘合关系与之对应，即“庞加莱多边形定理”。这些理论都使用具体例子加以逐渐深化的说明。

在论文末尾，庞加莱对富克斯群做了推广、大致分类和历史注记。

不过，从今天的观点看，在此文中庞加莱对其中某些定理的论证并不是完全严密的，例如富克斯群的存在性的证明后来被马斯基特（Maskit，1971）所严格化，其主要创见在于使用更现代的（点集）拓扑学理论，而不是庞加莱的手工（组合）方式去构造证明。而其中用生成元和关系刻画群的思想，随后被克莱因及其学生戴克（Walther von Dyck，1856-1934）等人做了发挥，成为组合群论的起源。

2.2.2《富克斯函数的研究》

第二篇Sur les fonctions fuchsiennes，即《富克斯函数的研究》

在理清了富克斯群及其基本域的相互关系后，庞加莱开始综述在富克斯群作用下保持不变的函数。他将这类函数称为富克斯函数。本文前两节处理的核心问题是：

（1）给定富克斯群，是否存在在这个群作用下不变的自守函数？

（2）给定富克斯群，如何构造对应的自守函数？

首先，我们回顾椭圆函数理论中魏尔斯特拉斯函数的构造。设Ω={11+22|1，2∈Z}是复平面上的一个格，定义魏尔斯特拉斯函数：

此处“对平移群的所有群元求和”使得函数在群作用下不变，而分母中指数为2使得求和收敛。另外，雅可比在1838年给出了函数的级数构造，它满足的性质是：(+)=(，)()，此处(，)是一个与无关的因子。他指出：如果两个不同的函数有相同的(，)因子，那么这两个函数的商就是椭圆函数。

与之类比，庞加莱敏锐地看到，给定富克斯群后，可以用以下方式构造自守函数：首先类比函数，构造所谓的-富克斯函数（theta-Fuchsian function），其形式为

其中为给定的富克斯群，群元遍历其中，为任意的有理函数，为正整数。与函数类似，-富克斯函数有两条重要性质：（1）当≥2时，级数在单位圆盘上绝对收敛（除孤立极点外）；（2）在群元作用下有：Θ(())=(+)2Θ(z)，其中()=。（在现代，此性质对应权为的“模形式”所符合的条件）。

然后庞加莱指出，如果两个对应于同一群的-富克斯函数，它们(，)因子相同，则其商就是在此群作用下不变的富克斯函数，并证明了其收敛性和其他一些性质。

在文章中，庞加莱虽然并未系统地引入双曲几何理论，但在很多关键部分本质地用到了双曲几何。例如，在证明自守函数收敛性时，文中提供了两种证明，其中第二种证明中本质性地用到了双曲平面的性质，即面积元之和有限导致级数收敛。再如，论文中的一个引理（第1节引理5）实质上是证明了实分式线性变换群作用在庞加莱圆盘模型上是等距的。

在此基础上，庞加莱用函数论方法处理了一些自守函数的问题：

（1）在富克斯群的一个基本区域内，零点和极点有什么性质？

（2）给定富克斯群，有多少（代数意义上）“极大独立”的自守函数？

（3）自守函数与二阶常微分方程解的关系？

以上问题在椭圆函数理论中都有对应的版本。

文中给出的结论是：（1）在富克斯群的一个基本区域上，零点和极点的个数均有限，且二者相等；（2）对于给定的富克斯群，任意两个自守函数1()和2()都是代数相关的，即存在多项式函数Φ(1，2)，使得Φ(1()，2())≡0；（3）其他相关结论，如富克斯函数与亏格和常微分方程的指数方程的关系。

其中的第（2）点又可引发一个深刻的问题：我们已知道对于给定的富克斯群，任意两个自守函数数1()和2()都代数相关，即存在多项式函数Φ(1，2)，使得Φ(1()，2())≡0。那么其在一定意义下的反问题是：

参数化问题：对以（代数）方程Φ(，)≡0联系着的复变量，，是否有函数1，2，使得=1()，=2()?

这个问题本质上联系着所谓的单值化问题，详见本文续篇《庞加莱在自守函数上的工作对其后数学的影响》。

2.2.3《关于克莱因群的论文》

第三篇Mémoire sur les groupes kleinéens，即《关于克莱因群的论文》

在这篇文章中，庞加莱处理了更加复杂的克莱因群。所谓克莱因群，是指复分式线性变换群(2，ℂ)的不含不变圆的离散子群。因为不含有不变圆，它不再能被看作双曲平面的等距变换群，故其性质要比之前研究的富克斯群复杂得多（参见下面的两张图）。甚至直至今日，克莱因群的丰富性质还是数学家们探索的对象。

图11克莱因在1881年给出的一个克莱因群的例子中的基本域，注意其中部分圆弧的边相切。图12：一个肖特基（Schottky）克莱因群的极限集。图源：弗里克和克莱因《自守函数讲义》中图145。

问题：应当如何研究克莱因群？

庞加莱研究克莱因群的方式是升维。虽然因为不存在不变圆导致一般的克莱因群不能看作双曲等距群的子群，但可以注意到，(2，ℂ)是扩充复平面的共形变换群，而扩充复平面又可看作三维双曲空间的边界。庞加莱发现，三维双曲空间（使用三维的庞加莱“上半平面”模型）的等距变换和其边界上的共形变换实际是一一对应的，具体对应方式是：上半平面中关于测地半球面（即赤道面在平面上的上半球面）的反演，一一对应于平面上的、关于该球面与平面之交圆的反演。而三维双曲空间的保向等距，和其边界上的共形映射，分别对应于关于上述两类球面或圆周的反演之复合，这样就建立起二者的一一对应。所以可以用三维双曲几何的观点来研究克莱因群。

之后，庞加莱类比第二篇文章，对克莱因群构造了-克莱因函数。与第一篇文章类似，在函数论方面平行的理论也被建立起来。

庞加莱对克莱因群的研究和分类，开后世之用克莱因群研究三维流形（见下图）的先河。

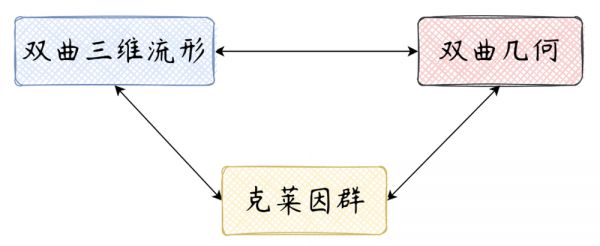
图13

他在此文中还引入了“极限集”等离散群理论中的重要概念。克莱因群的极限集可以是处处不可微的。“分形几何之父”曼德尔布洛特（1924-2010）曾指出，庞加莱对克莱因群的研究给出了分形的一个重要而自然的例子。（注：在后来数学家的著作[15]中，利用“等长圆”（isometric circle）观点可以更加统一地在复平面上处理富克斯群和克莱因群。）

2.2.4《关于线性方程的群》

在第四篇长文Sur les groupes deséquations linéaires，即《关于线性方程的群》中，庞加莱主要讨论以下问题：

（1）给定常微分方程，求其对应的单值化群（其含义参见本文第一部分的“常微分方程”章节的介绍和下文）；

（2）对于给定的（带有辅助参数的）二阶常微分方程，确定其单值化群是否是富克斯群。

论文的结构大致是：在前几章中，使用分析和线性代数的观点研究一般阶数的代数系数常微分方程，其形式为，其中和满足某种代数关系(，)=0，它是单值代数系数常微分方程的推广。庞加莱首先定义和研究了其代数不变量，具体定义方式仍然是：考虑微分方程的一组基本解在绕着奇点附近的闭路旋转一圈后得到的结果，用原基本解线性表出所对应的线性变换系数（参考本文第一部分中的“常微分方程”一节）形成的矩阵的特征值。如果选定另一组基本解，则对应的线性变换与原变换共轭（相似），因此特征值不变。庞加莱称之为“基本不变量”。紧接着他引述了富克斯和汉布格尔（Hamburger）计算“基本不变量”的数值方法，并研究了基本不变量的性质。之后，庞加莱转入集中研究二阶常微分方程（其中，满足一个代数约束条件(，)=0）。如果基本解的比()的反函数()是富克斯函数，则此方程称为“富克斯方程”，这是其中最重要的方程，庞加莱证明了“基本不变量”（的类型）可以完全确定“富克斯方程”。

接下来，庞加莱先后用拓扑和几何/组合的观点对此进行研究。这些研究的重点都是围绕着他提出的参数化问题：

如果两个复变量，以代数方程联系着，那么能不能找到另一个复变量，使得和都可以表示成的（单值全纯）函数？

这个问题庞加莱在第二篇长文中提到过，只不过在此处的上下文中，和分别对应常微分方程的复变量和它的解（即原论文中所谓的“积分”）。几何上的具体研究方法仍然是从多边形出发的组合方法，庞加莱使用的例子是，首先回顾高斯时代的三个奇点的情形（超几何函数），之后转向对四个奇点情形的分析，这些例子至今仍为经典。而拓扑学的方法则是所谓的“连续性方法”（论文第8节），从本质上来讲，它需要之后的点集拓扑学中“开区域”和“维数”的不变性的理论——它们于20世纪10年代初由布劳威尔（L.E.J.Brouwer，1881-1966）所建立，因此在庞加莱的时代也必然是不严格的，而且在使用过程中遇到了本质性的困难。

庞加莱在此文中还多少碰触到了泰希米勒（Oswald Teichmüller，1913-1943）空间（作为“富克斯群构成的空间”）和映射类群的概念（论文第13节），尽管他当时并没有像后来的数学家那样对它们进行深入而更加独立的研究。除此之外，对现代的研究者而言，这篇论文中的单值化问题也很能激发他们的兴趣。

2.2.5《关于克莱因群的论文》

第五篇Mémoire sur les fonctions zétafuchsiennes，即《关于克莱因群的论文》。

在这篇文章中，庞加莱主要研究代数系数常微分方程、其单值解及其级数展开与θ-富克斯函数的关系。首先他对代数系数常微分方程及其奇点进行了分类，接下来研究了常微分方程解的级数展开。

庞加莱定义的富克斯函数是一组满足正则性条件的函数数1()，2()，…，()，使得对任意，有，且对每个固定的，有。

对“-富克斯函数系统”的另一个定义是，它是指取定一个富克斯群后，一组满足正则性条件的单值函数数1()，2()，…，()，使得对于任意整数1，2，…，，行列式

为的富克斯函数（参考Sur les fonctions fuchsiennes（关于富克斯函数），法国科学院院刊，载于[9]）。

庞加莱研究了富克斯函数的级数展开，并证明了以下几个重要结论：

（1）富克斯函数必然满足代数系数的常微分线性方程。

（2）在整数充分大时，所谓级数的收敛性及其富克斯群作用下的性质，其中为任意有理函数，为在的逆变换下，函数对应的变换对应的矩阵元。

（3）在比较简单的情形，即所谓“第一类富克斯群”的情形下，任意富克斯函数可以表示成一个级数的级数与一个θ-富克斯函数的商。[“第一类富克斯群”的原定义是，对富克斯群基本域的每个边界顶点对应的抛物变换，即所谓“临界替换”（substitutions critiques），对应的“乘数方程”（l’équation aux multiplicateurs）的所有根都是单位复数，这等价于该富克斯系统对应的代数系数线性方程的每个奇点，其行列式方程（équations déterminantes）对应的根都是实数。]庞加莱还研究了更复杂的情况，即不是第一类富克斯群的情况。其中主要用了级数展开和经典的分析方法，也使用了一些双曲几何的观点（例如在证明级数的收敛性时）。

关于常微分方程，第四篇和第五篇长文的主要贡献是：

（1）证明代数系数线性常微分方程都可以用富克斯函数和θ-富克斯函数积分求解，它们都是单值的；

（2）给定对应同一富克斯群的富克斯函数()和()，可以构造常系数二阶微分方程，使得该富克斯函数的反函数()是其两个基本解之比（对于其逆命题，在更复杂的“克莱因群”情况下，庞加莱只使用例子加以说明而未给出完整证明）；

（3）对于给定的富克斯群，可以用级数展开定义无穷多个富克斯函数，它们是无穷多个有理系数常微分方程的解，而系数的奇点为两个有限点和无穷远点。

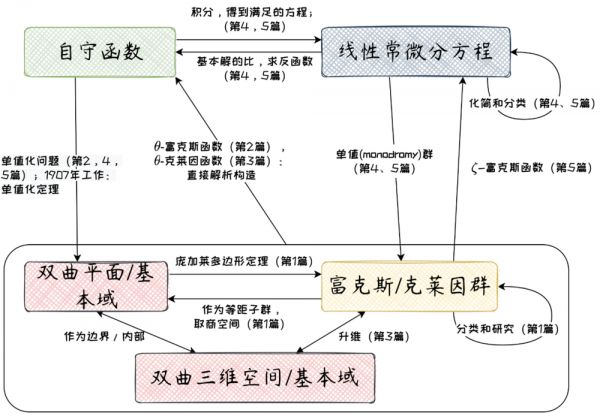
图14

庞加莱的这五篇长文在整体图景下的对应的大致位置可参考图13。可以看出，此时的整体图景与克莱因、庞加莱研究自守函数领域之前（参见本文第一部分《序曲》末尾）已有了很大差别。

3、庞加莱工作的突破之处

接下来，让我们从纷繁复杂、令人眼花缭乱的重重细节之中再次收回目光，看一下克莱因对庞加莱上述几篇文章贡献的总结。

根据克莱因的看法[1]，庞加莱在自守函数相关领域的贡献主要有以下三个特点：（1）（利用一般的富克斯群）“勇敢地”构造了最一般的基本域，而克莱因本人则受到了具体例子（例如p=3时用十四边形）和（用反演生成基本域的）具体方法的束缚；（2）庞加莱给出了自守函数的解析构造，即所谓庞加莱级数（或θ-富克斯函数）；（3）认识到这些新函数在单值化上的力量。

参考克莱因的以上意见，如果从更为宏观的角度看，庞加莱这些工作的突破之处至少有以下几个方面：

（1）提出自守函数作为椭圆函数、模函数和三角形函数的推广并给出了具体构造；

（2）富有创造力地在此课题中引入非欧几何观点，从而揭示了非欧几何（尤其是双曲几何）和单复变函数理论、微分方程的本质联系；

（3）将自守函数用于研究常微分方程理论（而相关的研究又为庞加莱之后关于常微分方程定性理论的研究提供了动机）；

（4）从上述研究中提出单值化问题，开启之后的单值化定理研究之序幕。

此处有一则有趣的轶事：因为克莱因曾经考虑过所谓的“富克斯群”，但富克斯本人却并没有考虑过它，因此克莱因对庞加莱表达了对这种命名方式的不满。作为回应，庞加莱把克莱因本人并未考虑过的一类函数称为克莱因函数。

4、庞加莱的创造过程与数学探索法

除了具体研究内容方面，在研究方法论和数学探索法上，庞加莱的研究还有如下特点，值得我们格外关注：

（1）在研究一般问题时，总是从具体的例子出发，然后通过不断深化研究，逐渐导向比较普遍的原理，而且在深化过程中仍然紧紧地抓住这些具体例子。

（2）用几何化的思想看待数学问题（包括分析领域的问题），在这个意义上，庞加莱可以看作自牛顿、黎曼以来的几何化传统的继承人。

（3）注重类比思维，并以此挖掘联系，例如将椭圆函数理论中由θ函数构造所求函数的方式，类比到自守函数领域；再将非欧几何中的变换与欧氏几何中的变换相类比；最终再建立自守函数的不变性与非欧几何中的变换群的联系，见图15。

（4）不因追求逻辑的完备性而牺牲原创性，其论文有的地方甚至不乏逻辑粗糙和不完备之处，但无损于其总体上的内在价值和惊人的启发性。

（5）尽力独立创作，例如在完全熟知黎曼的方法之前就自己发展出了类似的方法，这一点和克莱因形成了有趣的对比，后者十分熟悉文献、更侧重于博览群书，从总结和综合其他数学家的工作出发进行创造。

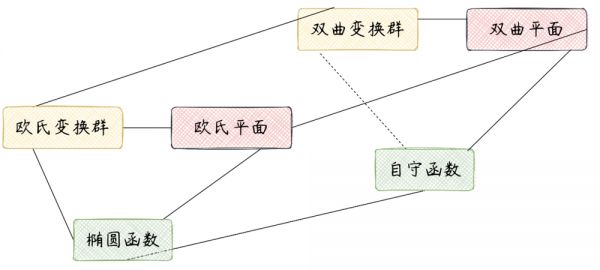
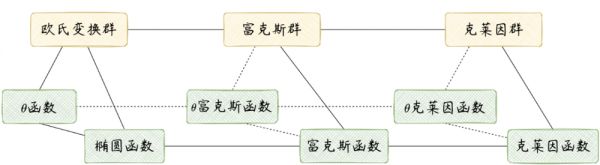
图15

关于庞加莱对创造过程的叙述，《返朴》公众号上还登载过苏联数学家庞特里亚金的文章《数学家的天赋体现在对形势的预判》，其中的逻辑和观点很值得我们参考。

最后，让我们以庞加莱的一段自述作为本节的结尾：

“我曾用了十五天时间力图证明，不可能存在任何类似于我后来称之为富克斯函数的函数。我当时一无所知；我每天独自一人坐在我的办公桌前，待一两个小时，尝试了大量的组合，什么结果也没有得到。一天夜晚，我一反平日的习惯，饮用了咖啡，久久不能入睡。各种想法纷至沓来；我感到它们相互冲突，直到成对地联结起来，也就是说，形成了稳定的组合。到第二天早晨，我已确立了一类富克斯函数的存在，它们来源于超几何级数；我只是必须写出结果，仅花费了几个小时。”

……

（在6月的马车之旅后）“然后，我把注意力转向一些算术问题的研究，表面看来没有取得许多成果，也没有想到它们与我以前的研究有什么关联。我为我的失败而扫兴，于是前往海滨消磨几天时间，想一些其他事情。一天早晨，当我正在悬崖旁散步时，一种想法浮现在我的心头，即不定三元二次型的算术变换等价于非欧几何学的变换，（这种想法）正好具有同样的简洁（brevity）、突然（suddenness）和即时确定（immediate certainty）的特征……”[11，13]

由此可见，即使庞加莱这样的大数学家都不乏错误的尝试（“花费两周证明富克斯函数不存在”）和整日思考、却因未有成果而颇感受挫的经历，那么我们广大数学爱好者和数学工作者还有什么可畏惧的呢！

那么庞加莱的这些工作对之后的数学产生了什么影响呢？且听下回分解。